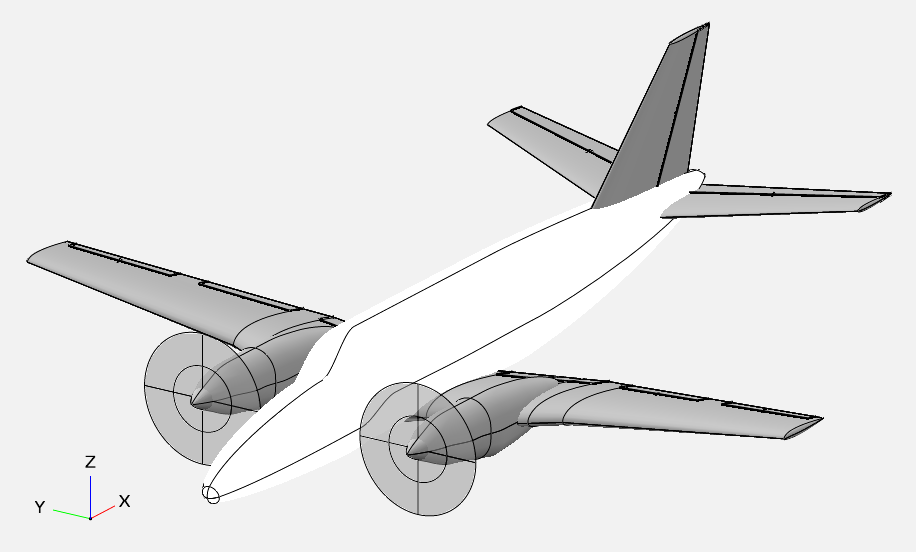
cover

飞行器动力学期末报告

March 9, 2022

    Aircraft Information

     

    Introduction

    The Beechcraft Model 99 is a civilian aircraft produced by the Beechcraft. The 99 is a twin-engine, unpressurised, 17-seat/15-passenger turboprop aircraft, with a unique nose structure used only on the 99. It was designed in the 1960s as a replacement for the Beechcraft Model 18 and its first flight was in July 1966. [2]

     

    Basic Data

    • Crew: One
    • Capacity: Normally 15 passengers
    • Length: 44 ft 6¾ in (13.58 m)
    • Wingspan: 45 ft 10½ in (13.98 m)
    • Wing area: 279.7 ft² (25.99 m²)
    • Height: 14 ft 4⅓ in (4.37 m)
    • Empty weight: 5,533 lb (2,515 kg)
    • Loaded weight: <10400 lb (4,717 kg)

     

    Major Performance

    • Cruise speed: 205 knots (380 km/h) at 10,000 ft (3,050 m)
    • Range: 910 nm (1,048 mi, 1,686 km) at 216 mph (347 km/h) at 8,000 ft (2,440 m)
    • Service ceiling: 26,200 ft (7,988 m)
    • Rate of climb: 1,700 ft/min (8.63 m/s)

    Aircraft Modeling

     

    Reference Data

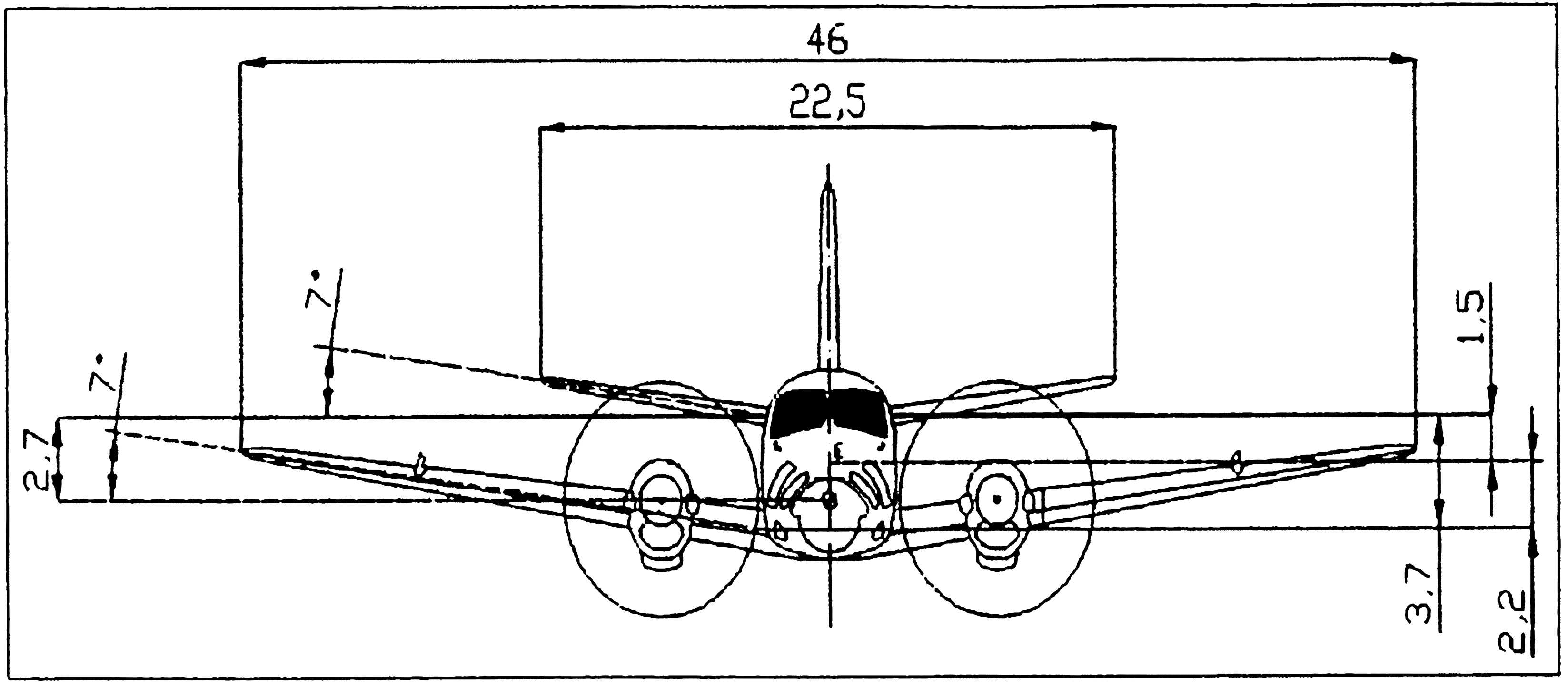
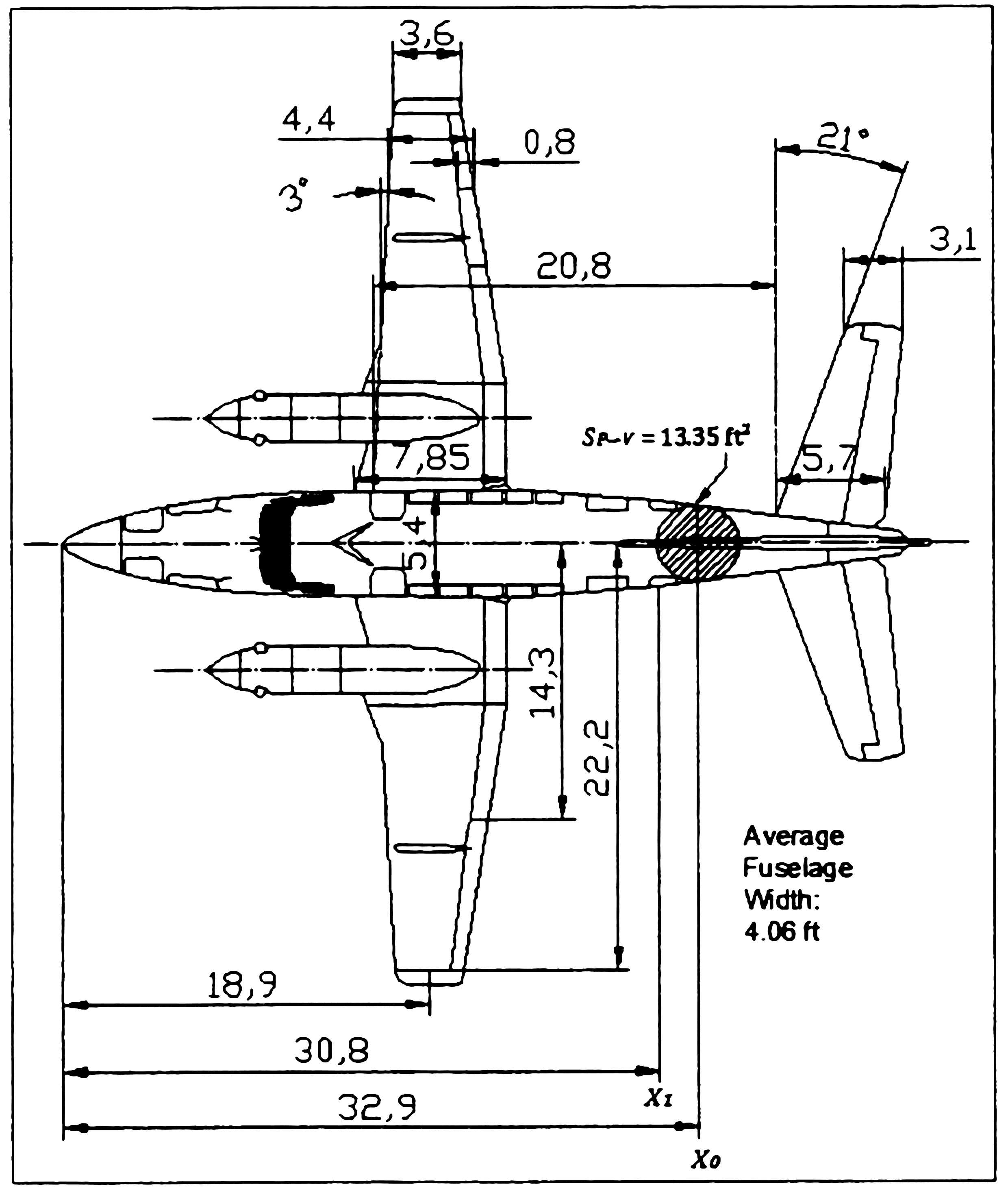
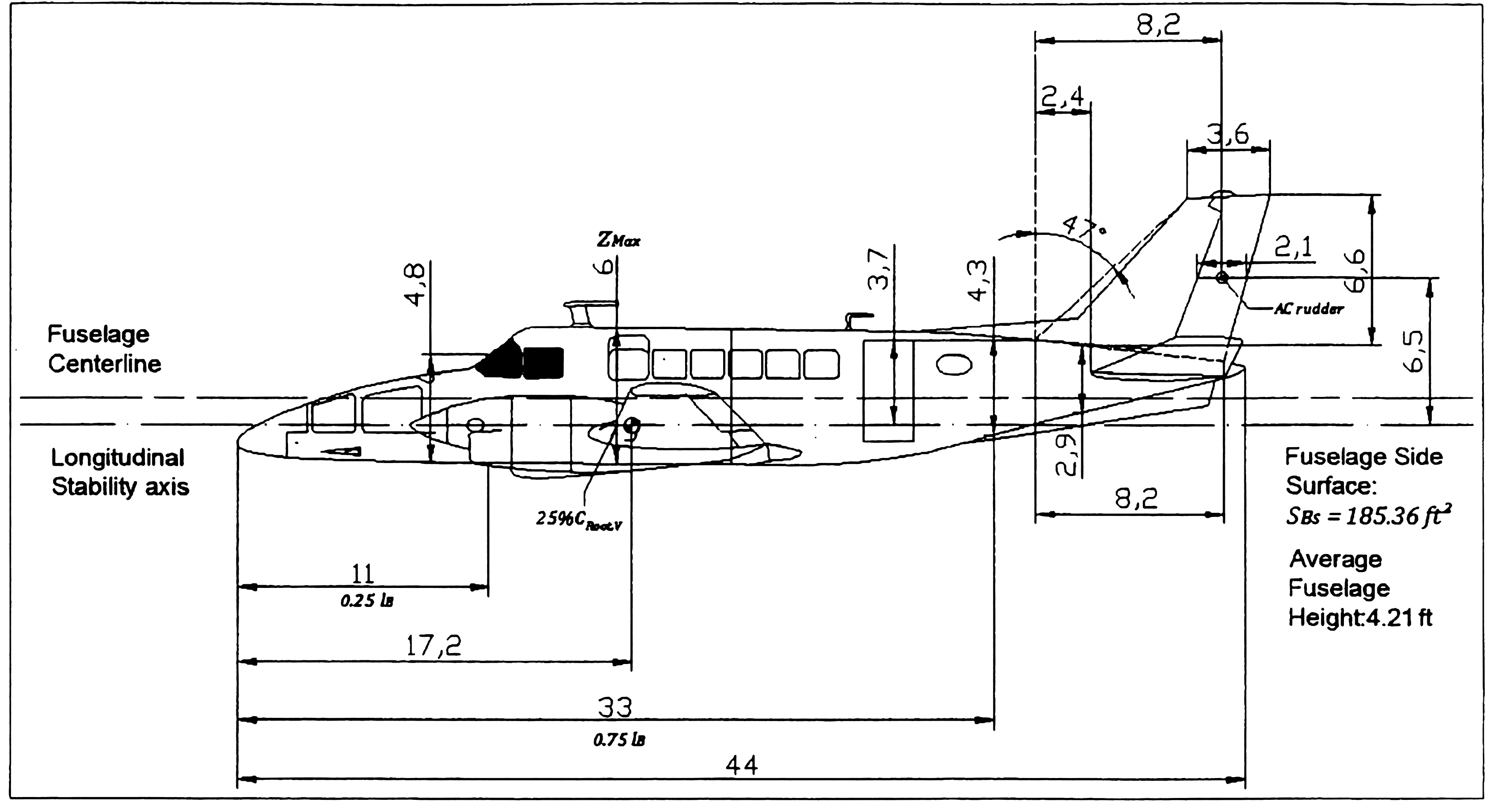
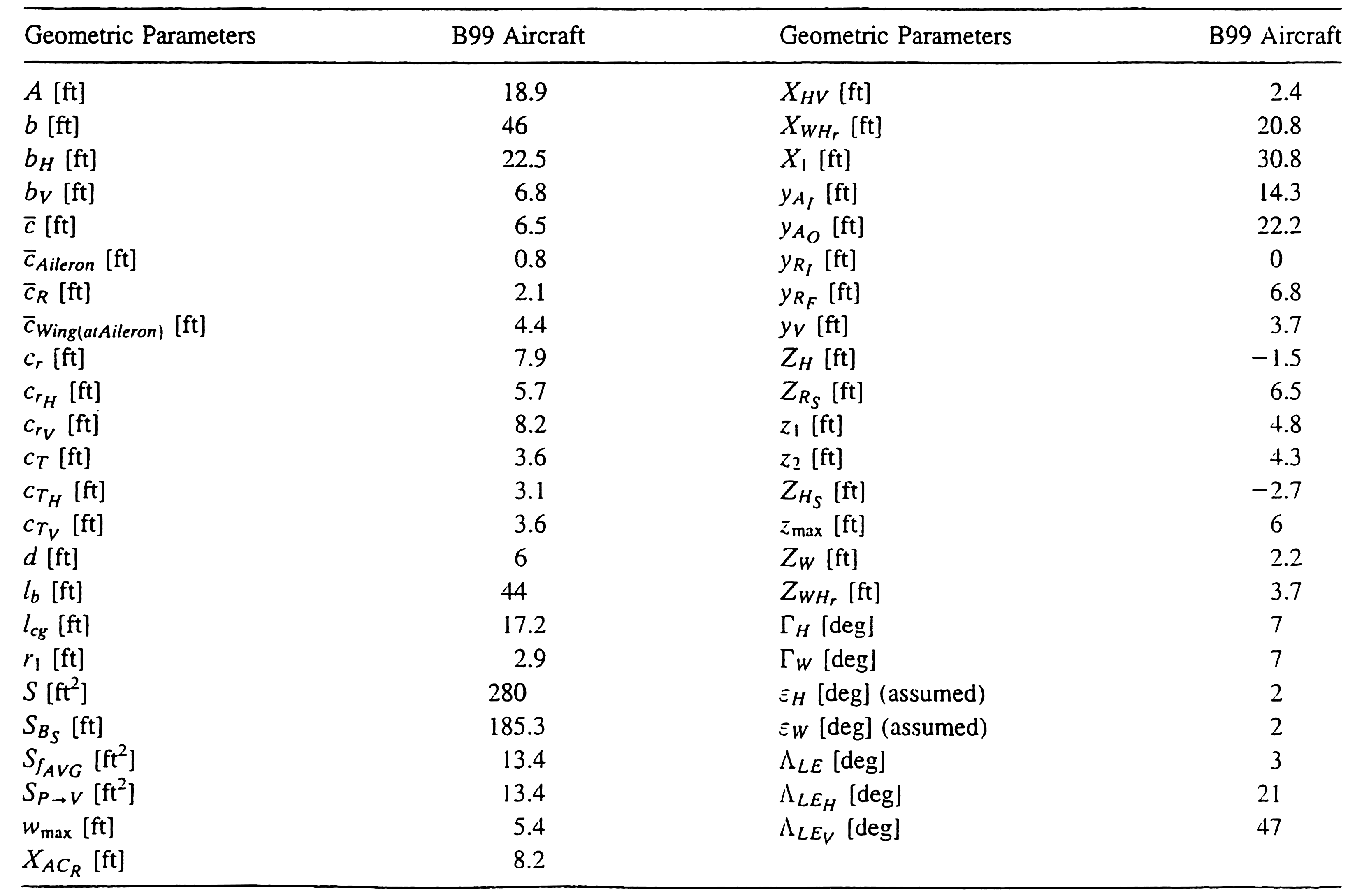
    In this porject, I use OpenVSP to model and simulate the aircraft. And compare some result with the linear model made by Jeff Scott, published in the https://m-selig.ae.illinois.edu/ads.html [3]. The linear data is in the appendex.

     

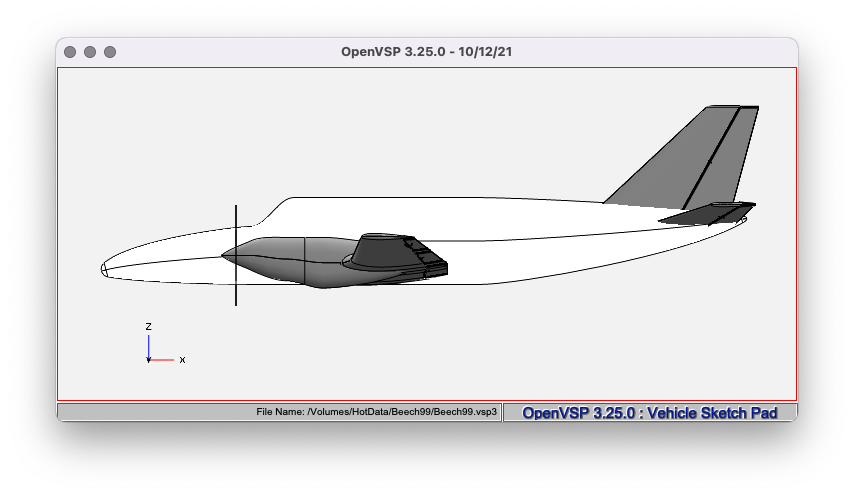
    OpenVSP Model

    The CAD and geometry data are posed in Appendex. The root airfoil is NACA 23018 and tip is NACA 23012.

    The model are shown below:

    Model1Model-top
    Model-frontModel-left

    Steady Flight

     

    Lift-Drag Ratio

    By the equation 5.24 [1] :

    $$ \left(\frac{L}{D}\right)_{\max }=\frac{1}{\sqrt{4 C_{D, 0} K}} $$

    First, we need $C_{D,0}$ . Calculate the $C_{D,0}$ from 0 to 0.4 Mach by VSPAero:

    C_D0

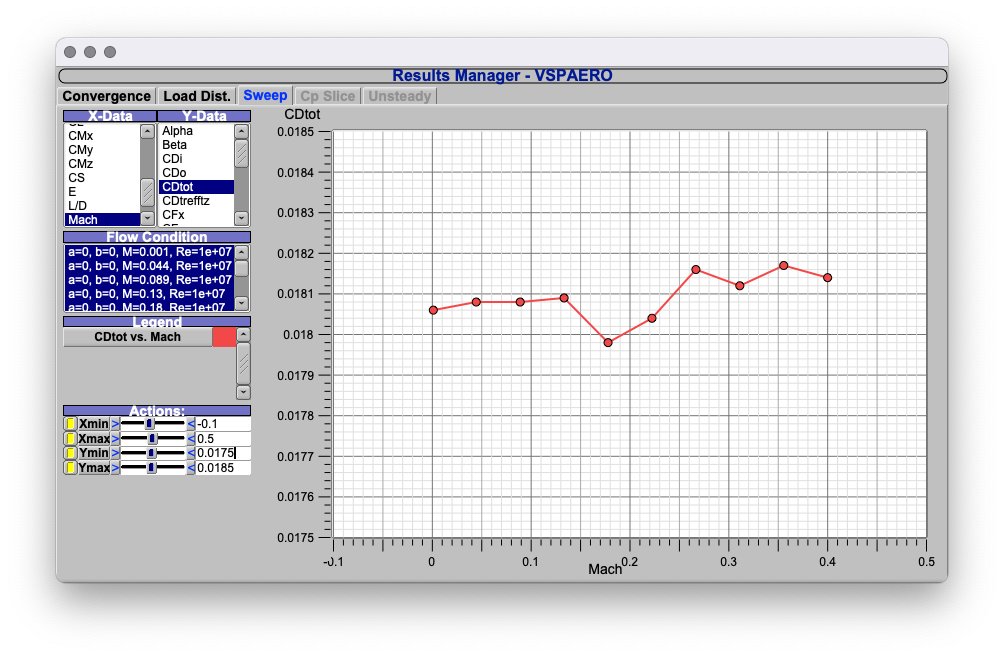
    So, the $C_{D,0} \approx 0.018$ .

    Use VSPAero to simulate the L/D varies from AOA:

    L:D-Alpha

    As shown in figure, the maximum of L/D is around 16 when $\alpha = 4 ^{\circ}$.

    Then, we know the $K \approx 0.055$ .

     

    Minimum Thrust

    From equation 5.21 [1] :

    $$ \left(\frac{T_{R}}{W}\right)_{\min }=\sqrt{4 C_{D, 0} K} $$

    $K = 0.055$, $C_{D,0} \approx 0.018$ :

    $$ \left(\frac{T_{R}}{W}\right)_{\min }=\sqrt{4 (0.018) 0.055} = 0.0629 $$

    Empty weight W = 6,000 lbs,

    $$ (T_R)_{\rm min} = 0.0629\ W = 378 \text{ lbs} \label{T_R_min} $$

    The velocity for minimum thrust and maximum L/D is:

    $$ V_{\left(T_{R}\right)_{min}}=V_{(L / D)_{max}}=\left(\frac{2}{\rho_{\infty}} \sqrt{\frac{K}{C_{D, 0}}} \frac{W}{S}\right)^{1 / 2} \\[6pt] =\left(\frac{2}{0.002377} \sqrt{\frac{0.055}{0.018}} \frac{6000}{280}\right)^{1 / 2} \\[6pt] = 178 \text{ ft/s} = 108 \text{ kts} $$

    According to the real-life velocity (see in the appendix), this speed is close to the best glide speed and best climb speed. Which match the property of maximum L/D.

     

    Maximum Velocity

    By the equation 5.50 [1], the maximum velocity can be calculated by:

    $$ V_{\max }=\left\{\frac{\left[\left(T_{A}\right)_{\max } / W\right](W / S)+(W / S) \sqrt{\left[\left(T_{A}\right)_{\max } / W\right]^{2}-4 C_{D, 0} K}}{\rho_{\infty} C_{D, 0}}\right\}^{1 / 2} $$

    We know the empty weight is 6,000 lbs, wing aera is 280 ft^2, maximum thrust is 1,550 lbs.

    From previous calculation, $C_{D,0} \approx 0.018$ and $K = 0.055$. Hence,

    $$ \text{Wing loading} =\frac{W}{S}=\frac{6,000}{280}=21.43 \ \mathrm{lb} / \mathrm{ft}^{2} $$
    $$ \text{Thrust-to-weight ratio} =\frac{\left(T_{A}\right)_{\text {max}}}{W}=\frac{1,550}{6,000}=0.2583 $$
    $$ V_{\max }=\left[\frac{0.2583(21.43)+21.43 \sqrt{(0.2583)^{2}-4(0.018)(0.055)}}{(0.002377)(0.018)}\right]^{1 / 2} \\[6pt] = 505 \ \mathrm{ft/s} = 299 \ \mathrm{kts} $$

    The result is beyond the real-life maximum velocity, which is 226 kts. Major reason is that the propeller can not maintain the max thrust at that speed. And plane can not fly with empty weight.

     

    Stall Speed

    By the equation 5.67 [1] :

    $$ V_{\text {stall }}=\sqrt{\frac{2}{\rho_{\infty}} \frac{W}{S} \frac{1}{\left(C_{L}\right)_{\max }}} $$

    Because VSPAero can not simulate flow separation, so I use the property of root airfoil (NACA 23018) from XFoil:

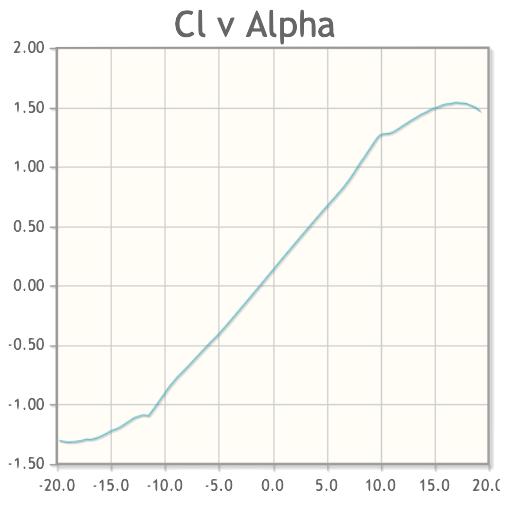
    Xfoil-root

    So, we assume the $(C_L)_{\rm max}$ occurs when $\alpha_{\rm stall} = 17 ^{\circ}$:

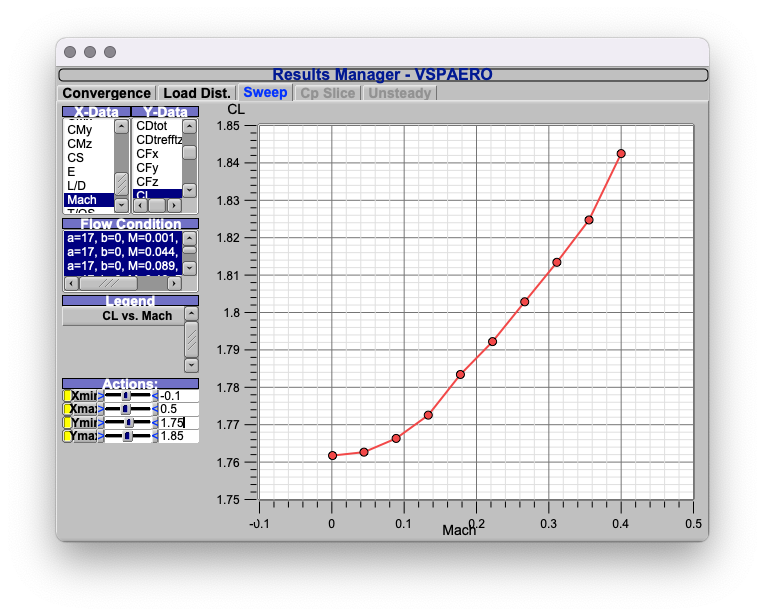
    C_L at a=17

    Then, the $(C_L)_{\rm max} \approx 1.8$ ,

    $$ V_{\text {stall }}=\sqrt{\frac{2}{0.002377} \frac{6000}{280} \frac{1}{1.8}} = 100\text{ ft/s} = 59\text{ kts} $$

    The result is close to the actual stall speed. Which is 65 kts. Because I use the empty weight, the result is smaller than real value.

     

    Climbing

    From the equation 5.94 [1] , we can calculate the maximum climb angle $\theta_{\rm max}$ :

    $$ \sin \theta_{\max }=\frac{T}{W}-\frac{1}{(L / D)_{\max }} $$

    Previous cases show that $T=1,550 \ \rm lbs$, $W = 6,000 \ \rm lbs$, $(L/D)_{\rm max} = 16$. So, $\theta_{\rm max} = 11.3 ^{\circ}$.

    Then, by the equation 5.98 [1] , the max angle-of-climb speed:

    $$ V_{\theta_{\max }}=\sqrt{\frac{2}{\rho_{\infty}}\left(\frac{K}{C_{D, 0}}\right)^{1 / 2} \frac{W}{S} \cos \theta_{\max }} \\[6pt] =\sqrt{\frac{2}{0.002377}\left(\frac{0.055}{0.018}\right)^{1 / 2} \frac{6000}{280} \cos (11.3^{\circ})} \\[6pt] = 176 \text{ ft/s} = 104 \text{ kts} $$

    Which is vary close to the real-life value 101 kts.

    The maximum rate of climb is:

    $$ (R / C)_{\theta_{\max }}=V_{\theta_{\max }} \sin \theta_{\max } = 34.5 \text{ ft/s} = 2070\text{ ft/min} $$

    Bigger than the actual rate of climb: 1,700 ft/min. Probably is that the actual climbing will not operate at the maximum angle-of-climb.

     

    Range

    As the Beech 99 is turbo-prop plane, we use equation 5.152 [1] :

    $$ R=\frac{V_{\infty}}{c_{t}} \frac{L}{D} \ln \frac{W_{0}}{W_{1}} $$

    And set conditions:

    • Fly at maximum L/D, which is 16.
    • Have the highest possible propeller efficiency.
    • Have the lowest possible specific fuel consumption.
    • Have the highest possible ratio of gross weight to empty weight.

    Data shows the fuel consumption is 74.6 GPH, and one gallon of jet fuel should weigh 6.7 lbs.

    The standard weight is 6,000 + 1,600 lbs. Using the minimum thrust equation $\eqref{T_R_min}$, we set the normal thrust is 500 lb.

    So the thrust specific fuel consumption:

    $$ c_t = \frac{500\text{ lb}}{500\text{ lb} \cdot 3600\text{s}}=2.8\times 10^{-4} $$

    Then, let gross weight $W_0 = 10,400\ \rm lb$, empty weight $W_1 = 6,000\ \rm lb$. The velocity for minimum thrust and maximum L/D is 178 ft/s.

    $$ R=\frac{178}{2.8\times 10^{-4}} \cdot 16 \cdot \ln \frac{10400}{6000} = 5.6 \times 10^6 \text{ ft} = 1707 \ \rm km $$

    The result is 1707 km and official maximum range is 1686 km. Considering the difference condition of range testing, this result match vary well.

     

    Endurance

    Use equation 5.167 [1] , we use the standard condition (1,600 lbs fuel):

    $$ E=\frac{1}{c_{t}} \frac{L}{D} \ln \frac{W_{0}}{W_{1}}=\frac{1}{2.8\times 10^{-4}} \cdot 16 \cdot \ln \frac{7600}{6000} \\[6pt] = 1.35 \times 10^4 \text{ s} = 3.75 \text{ hrs} $$

    Considering that we ignore the take-off, landing process and passengers. This result is close to the official value (2.9 hrs).

    Accelerated Flight

     

    Level Turn

    Use the equation 6.33 and 6.31 [1] at standard condition:

    $$ R_{\min }=\frac{4 K(W / S)}{g \rho_{\infty}(T / W) \sqrt{1-4 K C_{D, 0} /(T / W)^{2}}} \\[6pt] =\frac{4 (0.055)(7600 / 280)}{(32.2)(0.002377)(1550 / 7600) \sqrt{1-4 (0.055) (0.018) /(1550 / 7600)^{2}}} \\[6pt] = 402 \text{ ft} = 123 \text{ m} $$

    I can not find real-life minimum turning radius. But in the book, example 6.1 calculate a Gulfstream-like airplane which has minimum radius of 861 ft. Considering Gulfstream is turbojet plane and Beech 99 is turbo-prop plane. I think this is an reasonable result.

    $$ \left(V_{\infty}\right)_{R_{\min }}=\sqrt{\frac{4 K(W / S)}{\rho_{\infty}(T / W)}} = \sqrt{\frac{4 (0.055)(7600 / 280)}{(0.002377)(1550 / 7600)}} \\[6pt] = 111 \text{ ft/s} = 66 \text{ kts} $$

    This speed just over the stall speed (65 kts). It can be explained by intuition that smaller velocity can make a faster turn.

     

    Take off

    First, use the approx equation 6.95 [1] :

    $$ s_{g} \approx \frac{1.21(W / S)}{g \rho_{\infty}\left(C_{L}\right)_{\max }(T / W)}=\frac{1.21(7600 / 280)}{(32.2) (0.002377)(1.8)(1550 / 7600)} \\[6pt] = 1170 \text{ ft} $$

    1170 ft is way shorter than official distance 2480 ft. So, I guess the ground effect weaken the thrust. After calculation, we assume the thrust is 731 lbs.

    Then, we continue the calculation:

    $$ R=\frac{\left( V_{\rm R}\right)^{2}}{g(1.19-1)}=\frac{\left( 170\right)^{2}}{(32.2)(1.19-1)} = 4724 \text{ ft} $$
    $$ \theta_{\mathrm{OB}}=\cos ^{-1}\left(1-\frac{h_{\mathrm{OB}}}{R}\right) = \cos ^{-1}\left(1-\frac{50}{4724}\right) = 8.3 ^{\circ} $$
    $$ s_{a}=R \sin \theta_{\mathrm{OB}} = 4724 \cdot \sin(8.3 ^{\circ}) = 682 \text{ ft} $$

    So, the total take off distance $=s_g + s_a = 3162\text{ ft}$, approximately equal to the real distance 3200 ft.

    References

    [1] John D. Anderson, Jr. Aircraft performance and design.

    [2] https://wiki.flightgear.org/Beechcraft_Model_99

    [3] https://m-selig.ae.illinois.edu/apasim/Aircraft-uiuc/beech99-v1/

     

    Appendix

     

    Critical Velocity

      Meaning kts
    V_stall Stall Speed 65
    V_mca Minimum control speed in the air 85
    V_r Rotation Speed 100
    V_bg Best Glide Speed 100
    V_x Best Angle-of-Climb Speed 101
    V_y Best Rate-of-Climb Speed 120
    V_lo Maximum Velocity for Landing gear Operation 130
    V_le Maximum Velocity of Landing gear Extended 150
    V_a Manoeuvring Speed 165
    V_fe Maximum Flap Extended Speed 170
    V_no Velocity of Normal Operations 200
    V_c Cruise True Airspeed 205
    V_ne Velocity Never Exceed 226

     

    General Preformance

      Value   Value
    Takeoff Distance 2,480 ft Maximum Trust 1,550 lbs
    Takeoff Over 50 ft 3,200 ft Max Fuel Capacity 368 gal
    Landing Distance 1,810 ft Fuel Burn 74.6 GPH
    Landing over 50 ft 2,650 ft Endurance (full fuel) 4.4 hrs
    Service Ceiling 26,200 ft Endurance (1600 lb std) 2.9 hrs
    Empty Weight 6,000 lbs Range 910 NM
    Max Takeoff Weight 10,400 lbs    

     

    Engine Performance

    Condition Max HP Max RPM
    Take-off 550 2200
    Climb 538 2200
    Cruise 495 2200
    Idle   1800
    Acceleration   2420
    Reserve 500 2090

     

    Linear areo data

               
    CD_0 Drag Coefficient at 0 0.027 Cl_r Roll Moment Due to Yaw Rate 0.14
    CD_a Drag Curve Slope 0.131 CL_a Roll Moment Due to Aileron -0.156
    CL_0 Lift Coefficient at 0 0.201 Cl_dr Roll Moment Due to Rudder 0.0109
    CL_a Lift Curve Slope 5.48 C.G Center of Gravity Location 16%
    CL_adot Lift Due to AOA Rate 2.5 b Wing Span 46 ft
    CL_q Lift Due to Pitch Rate 8.1 c_bar Mean Aerodynamic Chord 6.5 ft
    CL_e Lift Due to Elevator 0.6 S Wing Surface Area 280 ft^2
    Cm_0 Pitch Moment at 0 0.05 l Aircraft Length 45 ft
    Cm_a Pitch Moment Due to AOA -1.89 I_xx Roll Inertia 10085 slug ft^2
    Cm_adot Pitch Moment Due to AOA Rate -9.1 I_yy Pitch Inertia 15148 slug ft^2
    Cm_q Pitch Moment Due to Pitch Rate -34.0 I_zz Yaw Inertia 23046 slug ft^2
    Cm_e Pitch Moment Due to Elevator -2.0 I_xz Lateral Cross Inertia 1600 slug ft^2
    Cl_beta Dihedral Effect -0.13 CL_max Max Lift Coefficient 1.75 /rad
    Cl_p Roll Damping -0.197      

     

    Airplane CAD

    CAD1

    CAD2

    CAD3

    Geom