甲烷喷流燃烧模拟

1. 引言

甲烷是最简单的也是含碳量最小的烷烃，是天然气的主要成分，约占天然气含量的 87%。甲烷燃烧具有环境污染小、放热量大等优点，但甲烷燃烧转化率受很多因素影响。因此，研究甲烷燃烧过程显得尤为重要。但利用传统的实验手段获得数据困难。在本次项目中，我们选择采用 Ansys Fluent 软件对实验过程进行了数值模拟。

本次项目针对无旋流、单喷嘴的圆柱形燃烧器进行三维瞬态数值研究，运用有限容积法建立甲烷和空气非预混燃烧与扩散模型，在相同工况下对比了不同的湍流模型和化学反应模型计算结果的不同。湍流模型分别使用 k-epsilon 和 k-omega 模型以及大涡模拟 (LES)。对于燃烧反应，使用了组分输运涡耗散模型以及非预混模型。

2. 模型及其边界条件

2.1 模型尺寸

本次模拟的对象为三维的简单圆柱形燃烧室，总直径 220mm，长 900mm；喷嘴外径 20mm，内径 10mm。中心截面的草图如下图所示。

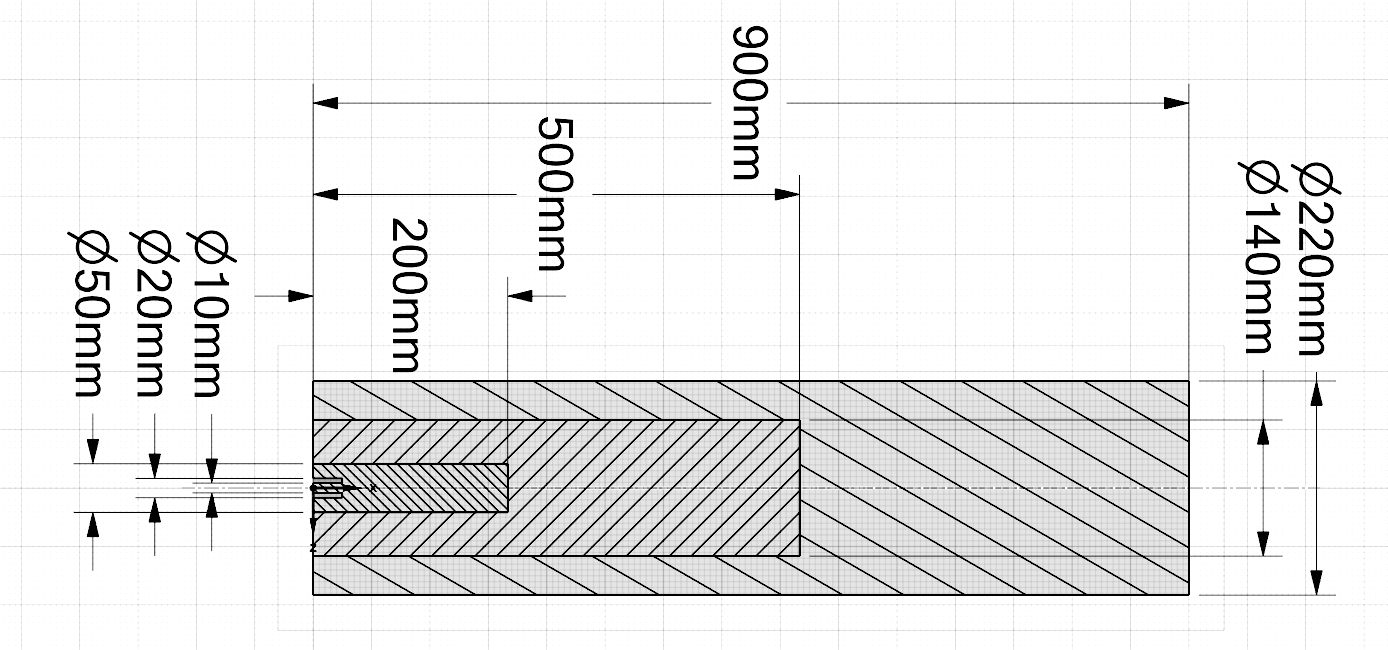
为了方便划分网格，建模时将模型分为三个部分，并整合为一个对象。

2.2 网格划分

使用 CutCell 方式划分网格，可以减少生成网格所需的时间。CutCell 网格将体积网格转换为以笛卡尔为主的网格（即网格主要由六面体元素组成，其面与坐标轴对齐）。在喷嘴附近使用较小的网格用于解析复杂细节，边缘使用较大网格减轻计算压力。不同元素大小为倍数关系，能较好衔接。

Mesh 设置 Method 为 CutCell，最大和最小单元大小分别为 8mm 和 1mm。在 Mesh 中插入两个 Body Sizing，分别选中核心部分以及中间层部分。将最中心部分单元大小设置为 2mm，中间部分为 4mm。添加 Named Sections，分别选中甲烷、空气入口以及燃烧室出口。节点数约为 43 万，单元数约为 40 万。划分结果如下图所示。

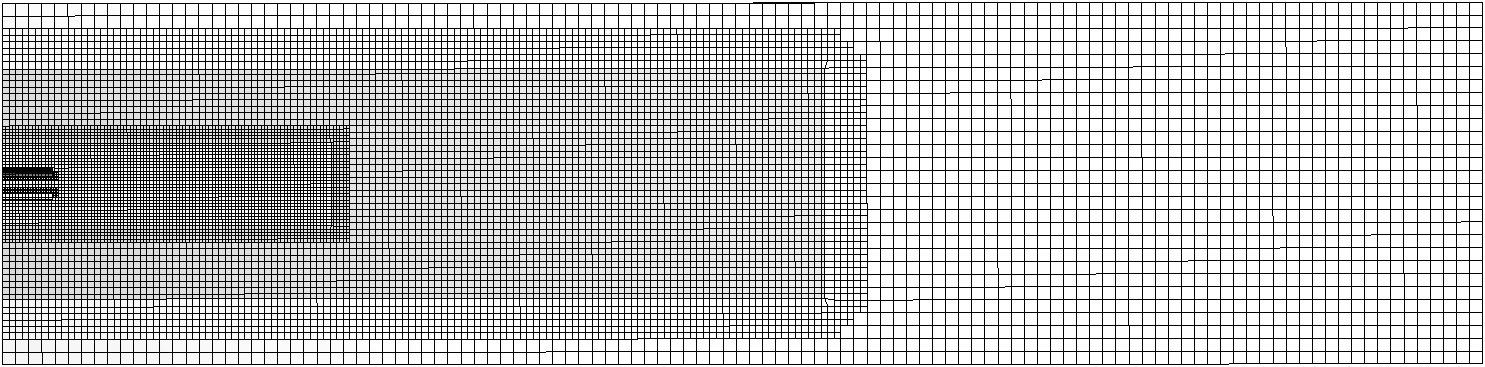
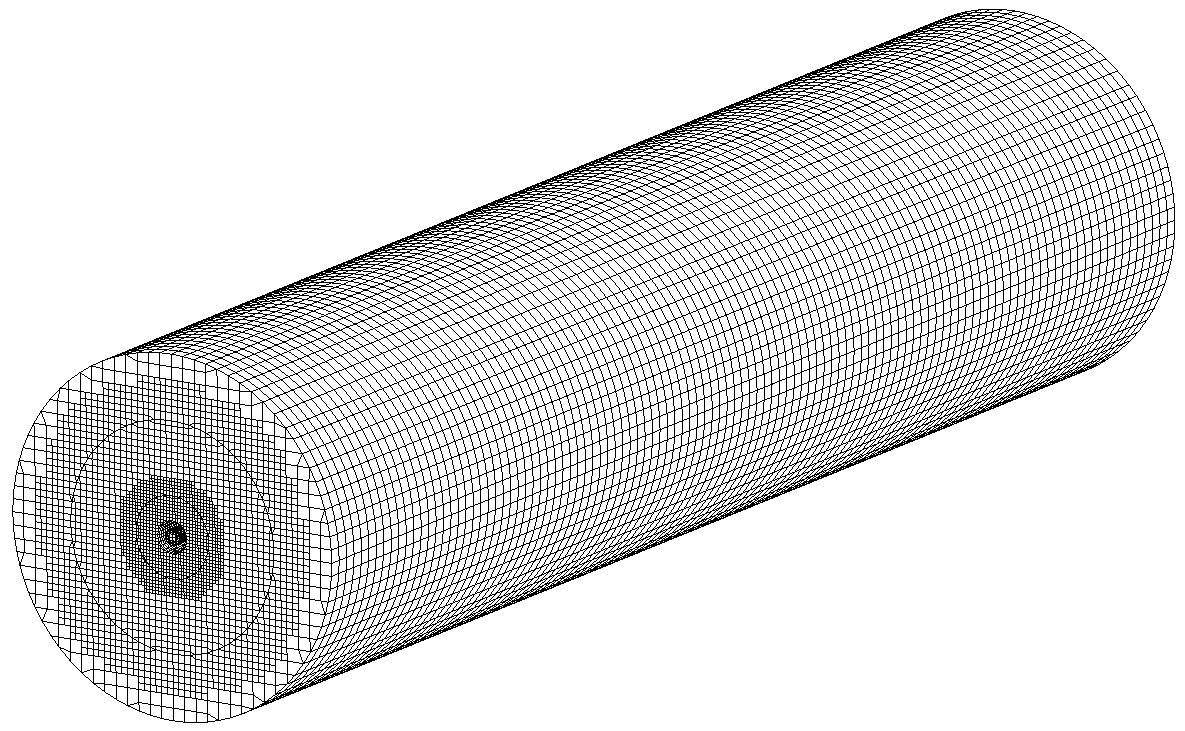
2.3 边界条件

将甲烷、空气入口设置为 velocity-inlet，空气流速为 0.5m/s，甲烷流速 50m/s，温度皆为 300K，添加预湍流强度 2%。出口设置为 pressure-outlet，表压为 0，回流温度为 1500K 便于计算收敛。其余表面都设置为 wall。

3. 数值模型及求解参数

3.1 湍流模型

k-epsilon 模型求解了两个变量：K – 湍流动能；epsilon – 动能耗散率。其具有很好的收敛速率和相对较低的内存要求，因此在许多工业应用中都颇受欢迎。但它不能非常精确地计算流动或射流中的逆压梯度和强曲率的流场。适合完全发展的湍流。

k-omega 模型类似于 k-epsilon，不过它求解的是 omega — 比动能耗散率。它的收敛难度较高，并且对解的初始猜测值非常敏感。因此，k-epsilon 模型常用于先行找出求解 k-omega 模型的初始条件。k-omega 对于 k-epsilon 模型不够精确的情况会非常有帮助，比如内部流动、表现出强曲率的流动、分离流，以及射流。

大涡模拟 (Large eddy simulation，LES) 是介于直接数值模拟 (DNS) 和 Reynolds 平均法之间的一种数值模拟方法。湍流包含一系列大大小小的涡团，目前所采用的最小尺度计算网格仍比最小涡大得多。大尺度涡决定了系统中动量、质量、能量及其他物理量的输运，小尺度涡几乎不受几何和边界的影响，它趋向于各向同性，且运动具有共性。LES 放弃全尺度范围上涡的瞬时运动模拟，只将比网格尺度大的湍流运动通过瞬时 N-S 方程计算出来，小尺度涡的作用表现为耗散。

3.2 化学反应模型

根据流动时间尺度与反应时间尺度的比值，即 Da 数，可大致将化学反应分为快速反应和慢速反应。若 Da>>1 时，我们认为化学反应特征时间远小于流动特征时间，反应物接触瞬间完成化学反应。仿真过程的反应速率由流动特征时间尺度决定，即湍流出现，认为燃烧开始且不需要点火源来启动燃烧。比如涡耗散模型 (Eddy-Dissipation Model)，以及 Fluent 中的预混、非预混模型。本次使用快速反应模型。

组分输运模型 (Species transport model) 计算物质输运方程，配合涡耗散模型即可模拟化学反应，反应速率由湍流混合速率决定。优点在于可以计算多种组分的混合，但同时计算开销较大。

非预混模型 (Non-premixed) 不计算组分的输运方程，只求解混合物分数及其方差的输运方程。其假设反应受混合速率控制，即已经到达化学平衡状态。每个单元内的反应使用概率密度函数法 (PDF) ，由燃料和氧化剂的混合强度所控制。

两个模型都适用于湍流、快速反应，缺点在于当混合和运动时间尺度大小相似时结果不可靠，以及点火熄火等细节现象无法模拟。

3.3 求解参数设置

项目设置为非稳态计算，开启能量方程。湍流模型都设置为标准模型，使用默认参数，其中 k-omega 开启 Low-Re 和 Shear Flow Corrections。大涡模拟开启涡耗散模型，设置化学反应为 Relax to equilibrium。

组分输运模型，使用甲烷-空气 2 步反应，在边界条件设置空气组分含有 23% 氧气，燃料组分为 100% 甲烷。非预混模型开启非绝热，使用默认空气组分，燃料组分设置为 100% 甲烷。

计算方法使用耦合二阶隐式算法，对湍流动能与湍流耗散率方程采用一阶迎风格式加速收敛，其他方程采用二阶精度格式。初始化使用标准模式，由所有区域计算初始值，并且在 x 方向添加 0.5m/s 的流速。计算时间步长为 0.0005s，600 步，最大迭代次数为 50。

4. 参考实验

4.1 Sydney 大学数据库

Sydney 大学 Masri 和 Bilger 等人建立了甲烷射流扩散火焰数据库^[1]，但是许多数据需要许可才能访问，开放的数据中相近的有旋流火焰。其实验设置为中心是孔状甲烷喷口，外侧为可调旋流环形空气喷口。其将火焰分为如下几种：

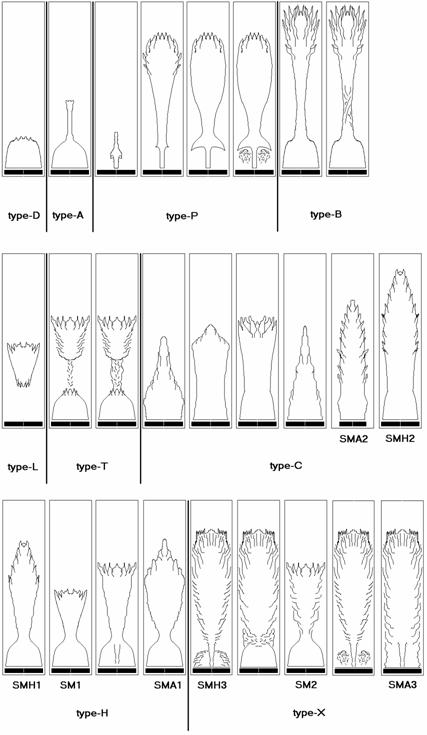
其中喷流速度为 66.3m/s 旋流数 0.66 的实验为 SMA1 型火焰，其他与本次计算条件相近的实验也为类似形状。

4.2 射流分区特性

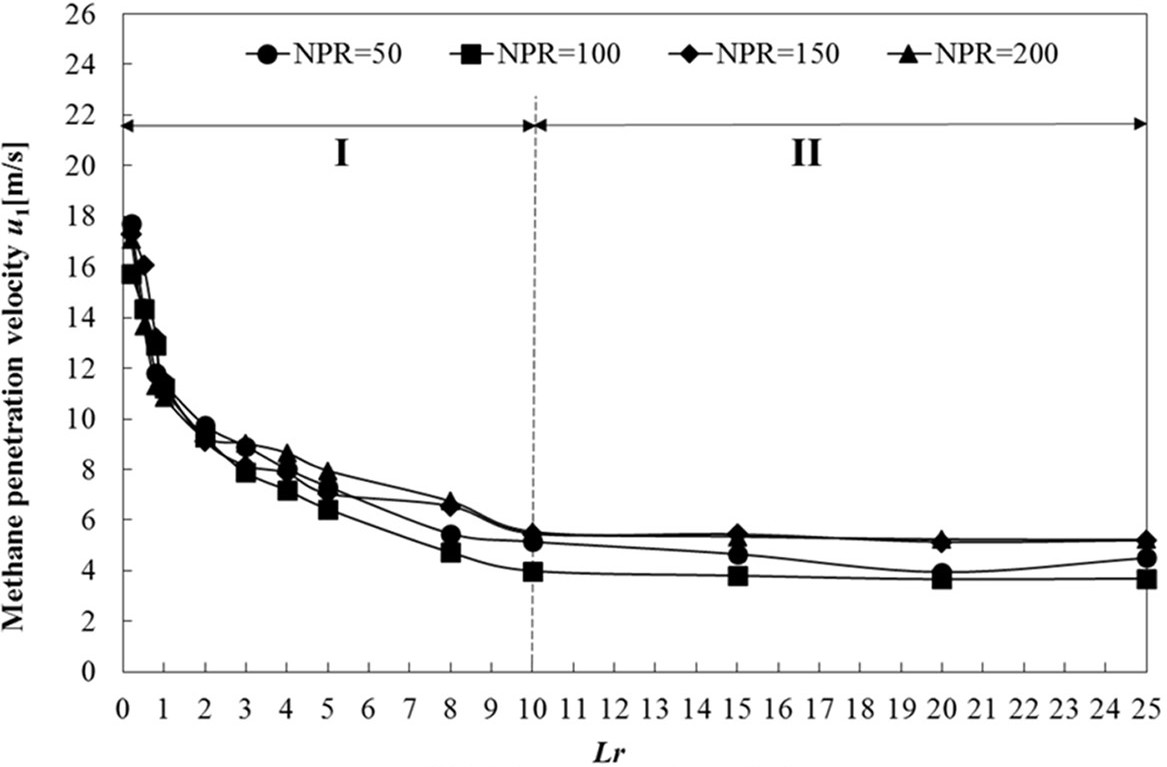
另一个文献是甲烷射流夹带特性的实验^[2]，其测量了非燃烧情况下甲烷离开喷口后的流动。甲烷气体射流的质量流速沿射流方向逐渐增加。高压甲烷气体射流的夹带过程可以分为两个区。在 I 区，即近场 (Lr < 10，Lr 为距离与孔半径比值)，甲烷射流质量流率随着 Lr 的增加而线性增加，然后达到最大值。在 II 区 (Lr ≥ 10)，射流质量和流速都恒定。其喷口直径为 1mm，甲烷压强从 5MPa 到 25MPa。本次计算设置的射流边界条件是恒定流速，压强远低于 5MPa，所以本次计算横向膨胀速度应小于此篇文献。另一个需要关注的区域是当 20 < Lr < 30。 Masri 和 Pope 认为，当射流扩散火焰不吹熄时湍流和化学反应最强的区域为下游 20-30 倍射流直径^[3]。

4.3 火焰结构

图 7 显示了甲烷喷射扩散火焰的实验结果，以及数值计算的结果。在图中，存在一个 Re 的临界值，约为 4000，超过这个临界值，在靠近喷射器的地方会不稳定，在混合层中产生一串大小递减的涡流，并触发所谓的混合过渡 (Dimotakis 2005)，变成完全湍流^[4]。

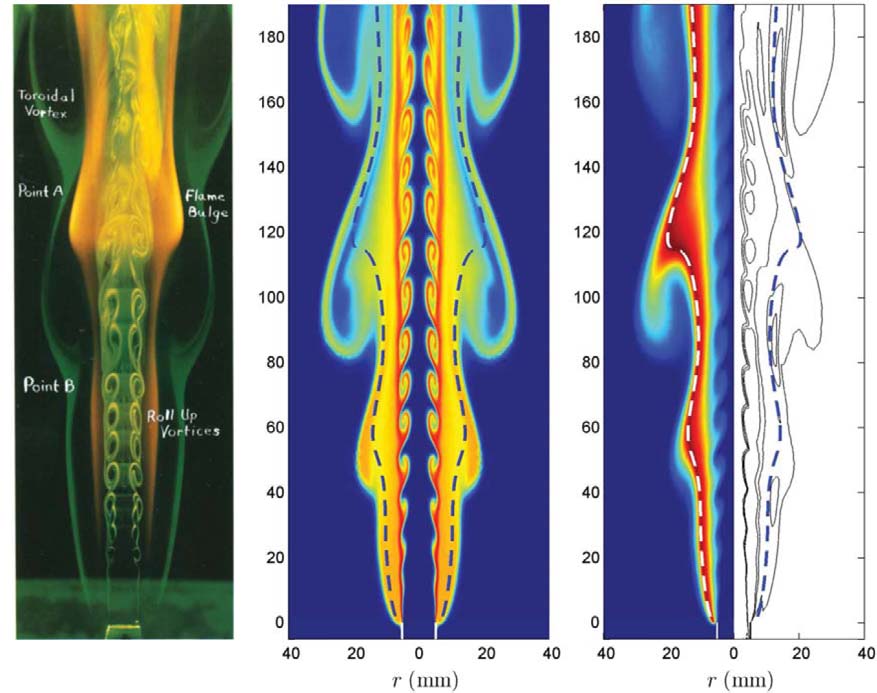
本次研究的雷诺数 $Re=2U_{0}a/\nu_{0}=17,000$，大于以上文献，其中 $U_{0}=50m/s$，$a$ 为喷口半径，$\nu_{0}$ 取甲烷在 400K 下的值。

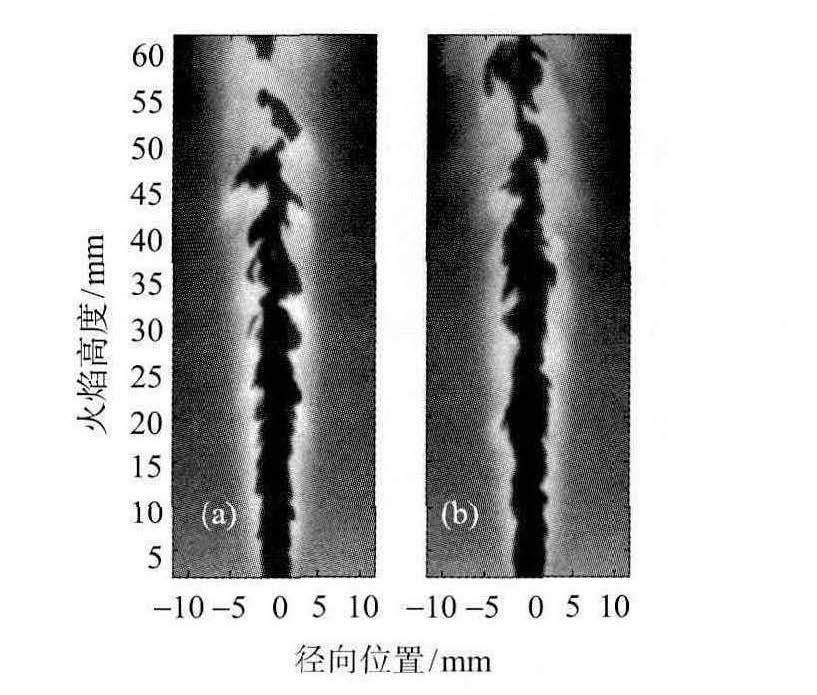
图 8 是翁武斌等人对甲烷湍流射流火焰锋面结构的激光测量图像，湍流火焰出口雷诺数为 10,681，其中气体为甲烷空气预混合气体，并且 (b) 有 10% 稀释氮气^[5]。

4.4 火焰组分分布

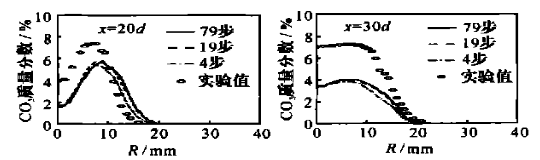
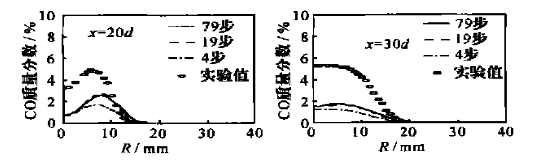
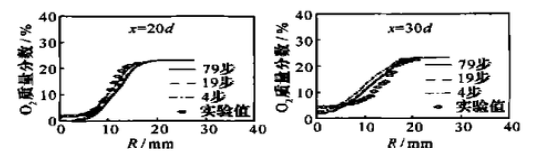
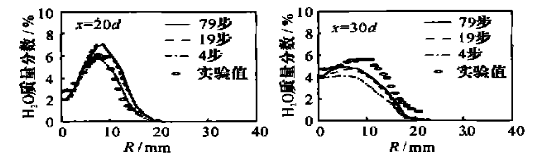
图 9 是董刚等人对相似情况的数值模拟^[6]，甲烷喷流速度为 41m/s，空气伴流速度 15m/s，在下游 20 和 30 倍射流直径处温度、氧气、CO2、CO和 H2O 的径向分布图：

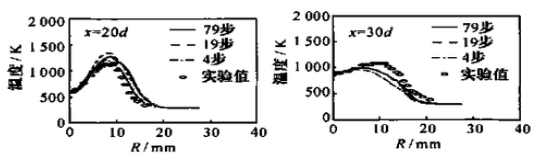
5. 计算结果及分析

本次研究以 LES 和 非预混模型为基准，结合实验数据，对比其他模型在瞬态计算时的差别。

5.1 不同化学反应模型对比

对比 0.015s 时两种反应模型的温度图像可以发现：非预混的湍流尺度较大，反应速度较快，在距离喷口较近的位置即完全混合并且反应；而组分输运整体反应速度较慢，射流延续了较远的距离。但是喷流前端没有出现甲烷/空气混合层的弓形区域。

对比 0.3s 时的温度图像：非预混的燃烧更快，而且温度也更高，最高达到约 2400K。相比之下，组分输运的最高温约 2200K。根据图 9，组分输运计算结果更符合实际，在 20 倍射流直径上更接近于 1500K。同时两者反应最强的区域都在 20 倍射流直径后。但是之后反应强度不减，原因在于空气流速设置过慢，反应不完全。

对比图 6，组分输运结果更符合「Lr < 10，射流质量流率随着 Lr 的增加而线性增加；Lr ≥ 10，射流质量和流速都恒定」，尤其是在近场有明显的线性增加区。而外侧的涡流形状也更符合图 7 和图 8 的形状，考虑到算例雷诺数远大于文献的临界雷诺数 4000，混合区直接发展为湍流。

同样根据图 6 ，减去设置的空气中 CO2 含量，组分输运的 CO2 结果符合实际。考虑到空气流速差别，CO 结果也较符合实际。非预混结果不符合实际。

组分输运的 O2 和 H2O 结果都符合实际，非预混结果不符合。我猜测这是由于非预混模型反应速度依赖于混合速率，而射流混合速率过快，Da 数接近 1，计算失准，化学反应过快。再加上其不计算组分输运方程，导致火焰扩散过快。而组分输运模型使用的涡耗散模型的反应速度依赖于湍流强度，并且组分输运单独计算，不会因不准确的化学反应而扩散过快，相比下更准确。

5.2 不同湍流模型对比

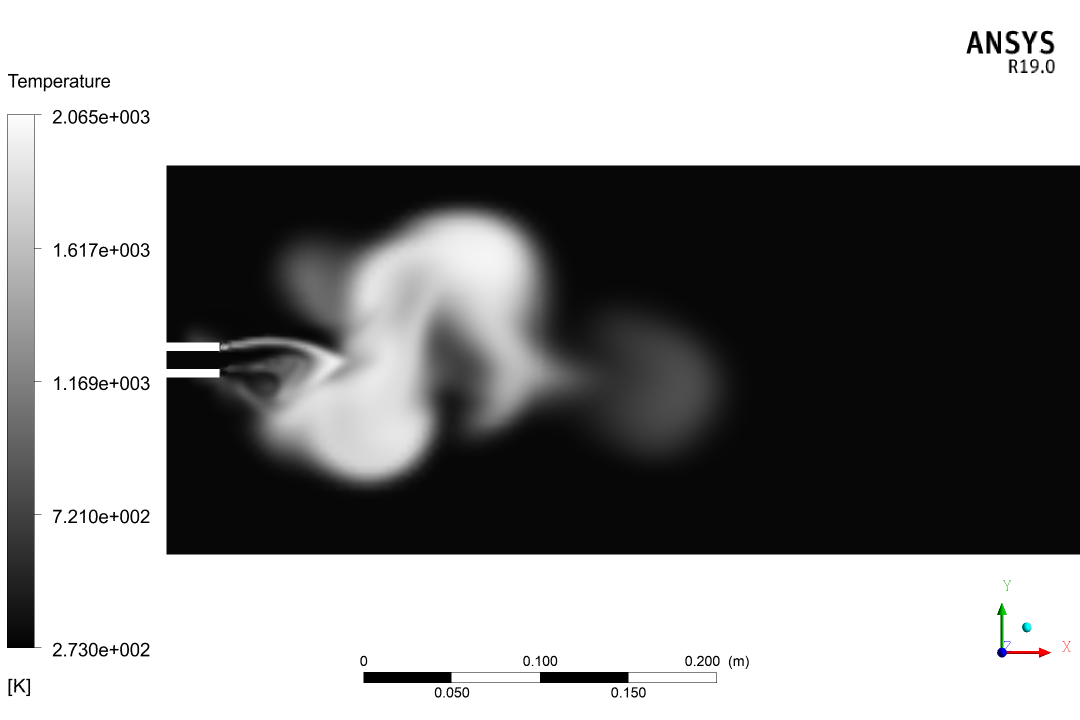
在射流起始阶段，由于 k-epsilon 不能精确地计算射流中的逆压梯度和强曲率的流场，计算结果不符合实际。相比之下 k-omega 就能比较好的展现射流的流动，并且相比基准方法，喷流前端有甲烷/空气混合层的弓形区域，但是相比文献，两侧燃烧强度超出了实际。

经过一段时间发展，k-epsilon 也能稳定下来，但是壁面附近产生了大量回流。猜测是由于壁面网格太大，并且没有做修正，导致边界层计算错误。两者的火焰温度都符合实际，除了 k-epsilon 结果中的回流区域。另一点是 k-epsilon 的甲烷/空气混合层角度更大。

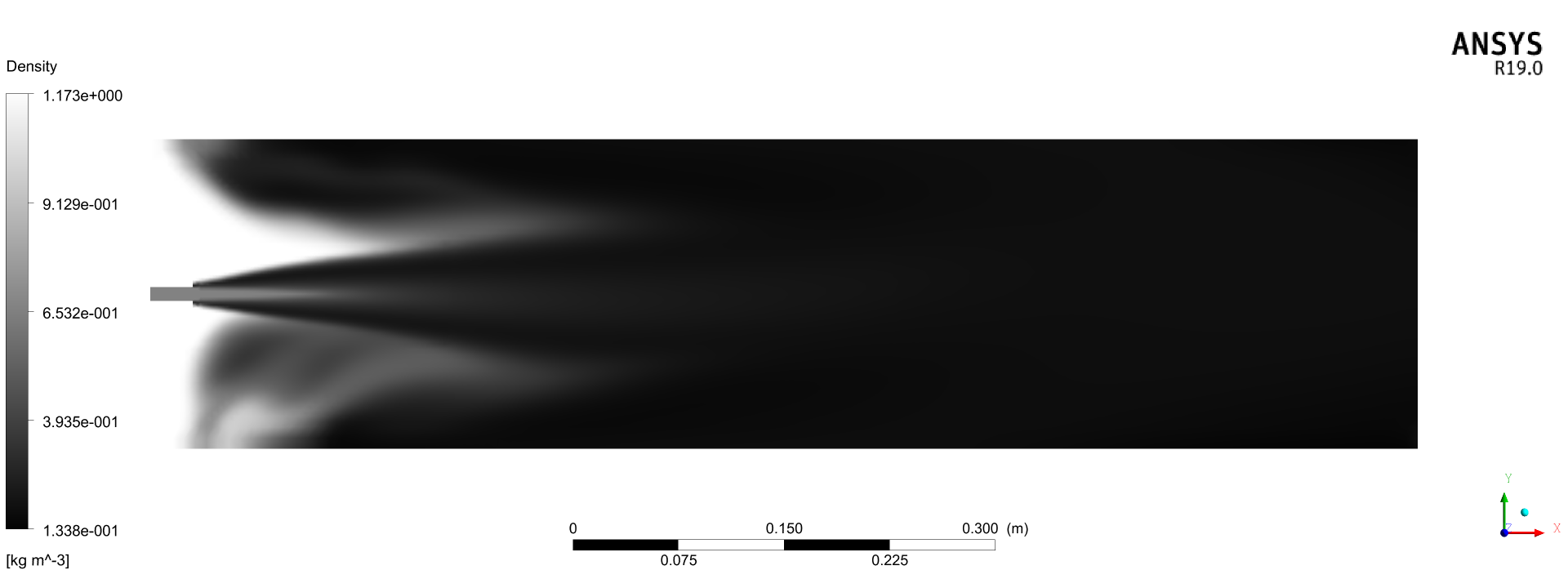
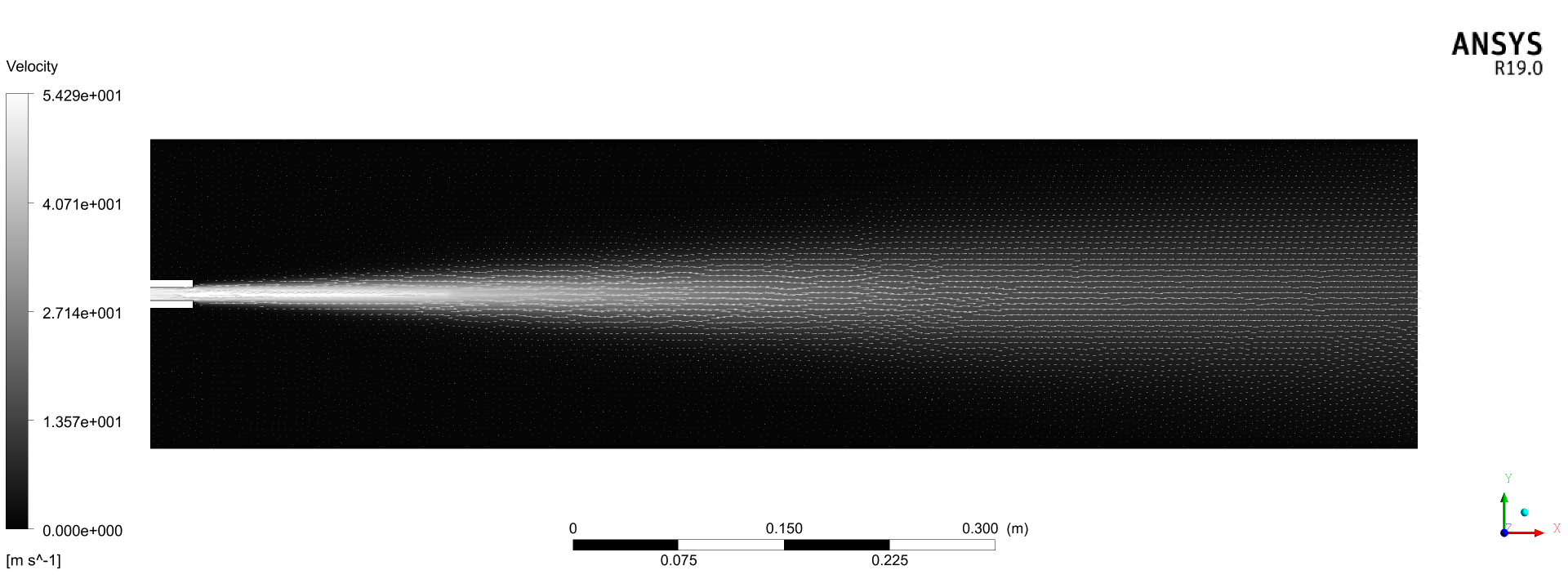
对比图 6，两者都符合「Lr < 10，射流质量流率随着 Lr 的增加而线性增加；Lr ≥ 10，射流质量和流速都恒定」，k-epsilon 的临界距离更接近 Lr = 10，喷口附近的扩散也更加线性。相比基准方法，两者都更符合远场恒定射流质量和流速。

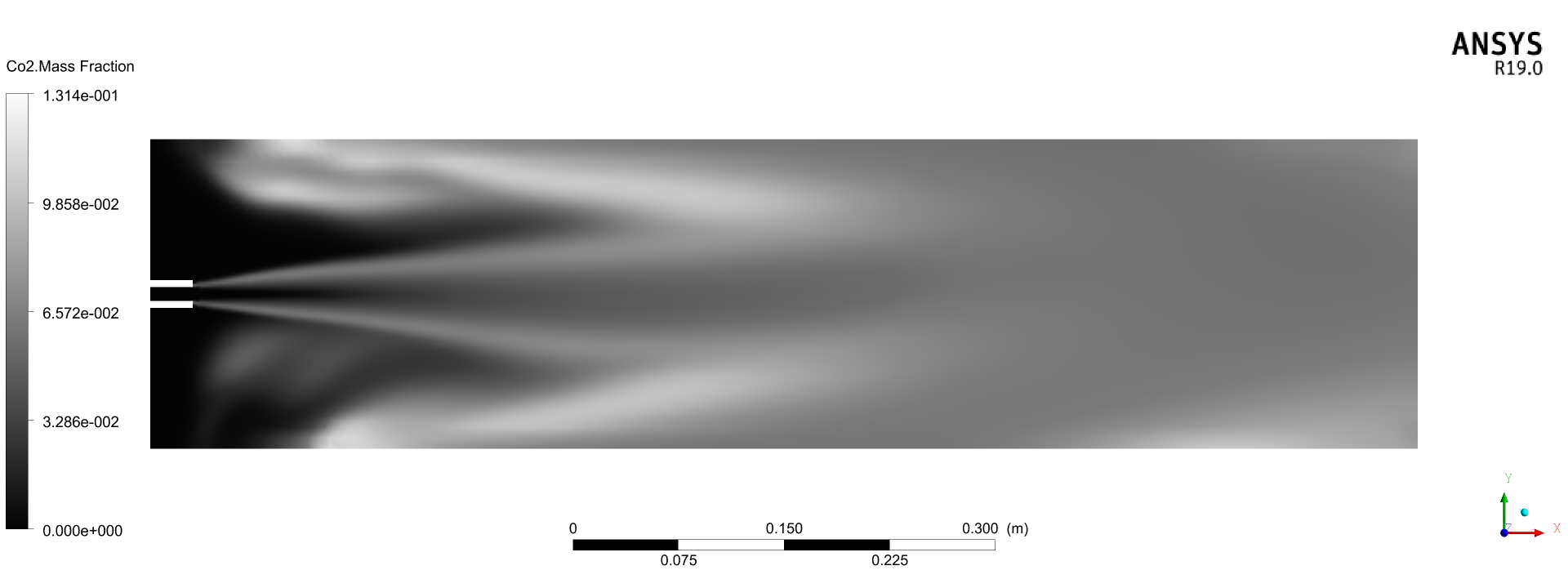
图 18 和 19 的组分分布与使用 LES 组分输运结果类似，都比较符合图 9 的实际数据。相比之下 k-omega 更为准确。

5.3 不同计算方法耗时

在相同网格划分、求解精度以及计算机配置的情况下。k-epsilon 非预混耗时 8.47 h，k-omega 非预混耗时 3.73 h，LES 非预混耗时 9.20 h，LES 组分输运耗时 3.85 h。

6. 项目总结

本次实习中，我学习了使用 Fluent 进行简单的瞬态燃烧数值模拟。在不断试错过程中学习了网格划分、不同的湍流模型和化学反应模型。以 LES 和非预混方法为基准，经过计算、对比、总结其他三种方法，得到如下几点结论：

1）基准方法 LES 和非预混比较糟糕，没有精细调整下，计算结果偏离实际情况较多。

2）LES 和组分输运在多方面都优于 LES 和非预混。气体流动准确度大幅提高，温度和主要反应产物准确度略高，计算耗时不到基准的一半。不过化学反应从 4 步简化至 2 步，所以无法分析中间产物以及污染物的产生。

3）k-epsilon 和非预混不是一个好的替代方案。在默认参数以及较粗糙的壁面网格下，k-epsilon 靠近壁面的计算结果不符合实际，只有喷口附近的流动和化学反应符合实际数据；而且计算耗时只比基准减少了 8%。

4）k-omega 和非预混优于基准方法。开启 Low-Re 和 Shear Flow Corrections 后，其在喷流初始阶段的计算结果是四种方法里最符合实验的，模拟出了喷流前端的甲烷/空气混合层的弓形区域。其他方面除了无法模拟出涡结构，都接近甚至优于 LES 和组分输运的结果。并且相较于 LES 和组分输运，可以计算更多的中间产物以及污染物，对于研究清洁燃烧以及高效燃烧有更大作用。同时计算耗时为最少，仅使用基准时间的 41%。

本次研究虽然选题简单，但对于不熟悉计算流体力学、也没学习过燃烧学的我是一个不小的挑战和宝贵的学习过程。而且对于点燃过程，还没有足够的知识和能力进行仿真，所以本次计算结果的发展阶段与实际情况有较大偏差。最后感谢指导老师在本次实习中的教导以及支持，我会带着本次的成果继续学习知识。

7. 参考文献