Stability of Cylinder Flow Based on the Energy Gradient Theory

Introduction

The study of fluid flow around a cylinder, and the subsequent wake, is a classic fluid mechanics problem. This phenomenon, often seen in natural scenarios like water flowing past a bridge pier, is characterized by periodic vortex shedding in the wake at a sufficient Reynolds number. These vortexes can induce unsteady loads on the object, making the study of flow separation and vortex shedding crucial.

Von Karmam was the first to analyze this phenomenon in 1912, establishing a relationship between vortex structure and drag on the cylinders. Subsequent research by Taneda [1-2] and Zdravkovich [3] further explored the physics of cylinder flow. Taneda's experiments revealed that Fopple eddies occur at a Reynolds number of 5, with the eddies lengthening and vortex shedding frequency increasing as the Reynolds number rises.

This report uses Computational Fluid Dynamics (CFD) to simulate parameter distributions in a cylinder flow field between two walls for Reynolds numbers from 1 to 100. The formation of the Karman vortex street is investigated using the energy gradient theory.

Methodology

Fluid dynamics simulations fall into two categories: conventional NS equation solvers based on macroscopic variables (velocity and pressure), and particle-based mesoscale methods like LBM and the molecular dynamic method. Unlike the conventional NS method, LBM represents fluid through particle distributions, from which macroscopic variables can be evaluated. LBM has several advantages over the conventional NS solver, including avoiding the Poisson equation in pressure evolution and easier implementation and parallelization due to its locality of computation. It is also inherently time-dependent, making it suitable for unsteady flow simulation.

Here's the depiction of our computational domain. We're dealing with a two-dimensional flow field, where the cylinder's axis is perpendicular to the flow direction. The cylinder has a diameter denoted as D. The overall computational domain measures 35D in length and 5D in height. From the cylinder's center, the upstream length is 10D, and the downstream length is 25D.

In this plot, we validate the grid independence at Re=100 by using three different grid sizes: NY=125, 256, and 512. By calculating the drag coefficient (Cd) for each, we find that the results vary by less than 0.5%, demonstrating the grid independence of our simulations. For later calculations, NY=256 is used.

Flow separation

Next, we visualized the flow fields for Re=1, 5, 10. These visualizations demonstrate the formation of recirculation behind the cylinder due to flow separation.

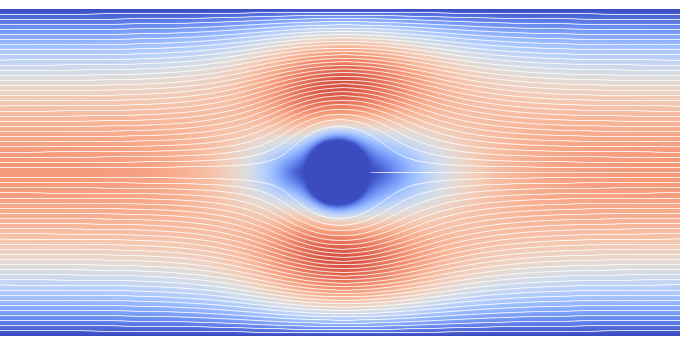
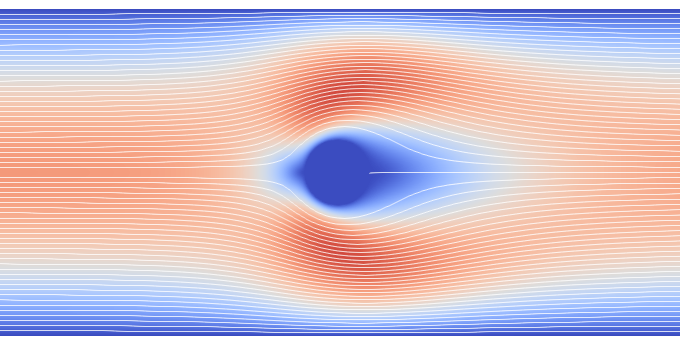
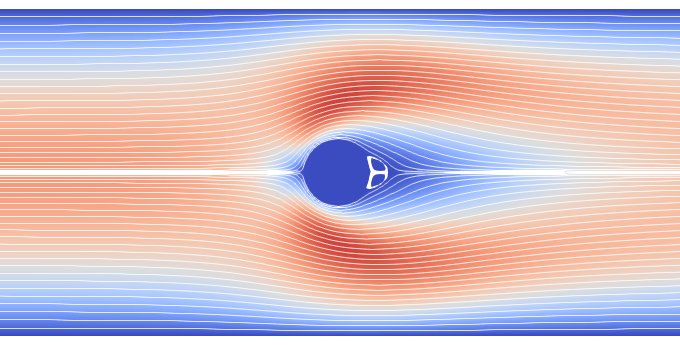
Unstable point

Firstly, we conducted simulations for a range of Reynolds numbers from Re=1 to Re=100. We observed that the flow begins to destabilize after Re=50. A plot illustrating the variation of drag and lift fluctuations with the Reynolds number is presented,

The amplitude of lift is fitted by parabola curve [6] and drag is fitted by power curve.

Here, we present a series of vorticity plots for Re=1, 10, 40, and 100. However, it is not straightforward to identify regions of flow instability from these plots. Therefore, it is needed to proceed with the energy gradient theory.

Energy Gradient Theory

The energy gradient theory, proposed by Dou et al. [4-5], is used to study turbulent transition and flow stability. This theory, based on Newtonian mechanics and compatible with Navier-Stokes equations, has been used to determine flow stability and turbulent transition with good agreement with experiments. The theory suggests that the transition to turbulence depends on the relative magnitude of energy gradient amplification and viscous friction damping under a given disturbance. When the ratio reaches a critical value, flow instability may occur.

The critical value of $K_{max}$ at subcritical turbulent transition for wall bounded parallel flows is $K_c=370-389$ [4]. This indicates that flow transition won't occur when the dimensionless parameter $K_{max}$ is less than $K_c$ in the flow field, otherwise it depends on the disturbance.

According to the energy gradient theory [5], the equation of the dimensionless parameter K can be written as:

$$ K=\frac{\partial E / \partial n}{\partial E / \partial s}=\frac{\mu\left(\frac{\partial^{2} v}{\partial x^{2}}+\frac{\partial^{2} v}{\partial y^{2}}\right) \cos \alpha-\mu\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}\right) \sin \alpha+\rho v\omega_z \sin\alpha+\rho u\omega_z\cos\alpha}{\mu\left(\frac{\partial^{2} v}{\partial x^{2}}+\frac{\partial^{2} v}{\partial y^{2}}\right) \sin \alpha+\mu\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}\right) \cos \alpha} \\[6pt] \cos\alpha=\frac{u}{U},\quad\sin\alpha=\frac{v}{U},\quad\omega_z=\frac{dv}{dx}-\frac{du}{dy} $$

Instability

Below, we showcase the maps of the energy gradient parameter K for Reynolds numbers of 1, 10, 40, and 100. Particularly, we can see the emergence and growth of high K value regions, indicating areas of potential instability.

Subsequently, we focus on the energy gradient parameter K for Re=49.

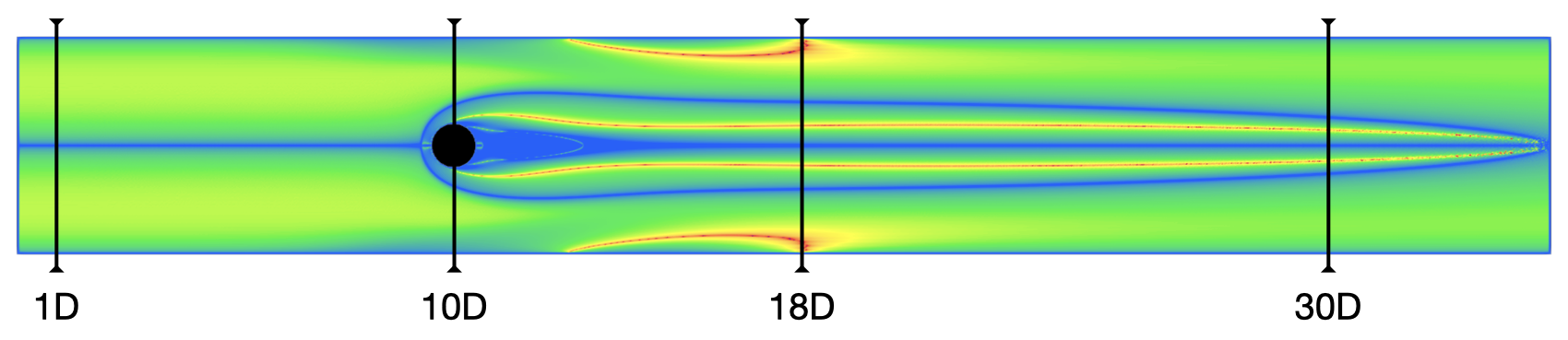
Examine the K value slices at x=1D, 10D, 18D, and 30D for Re=49.

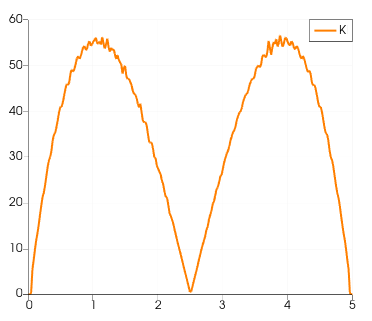
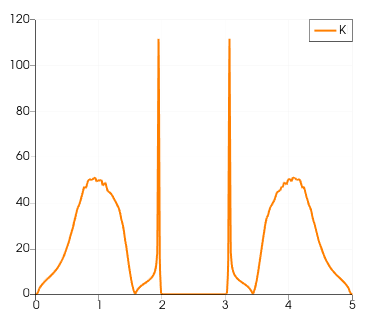
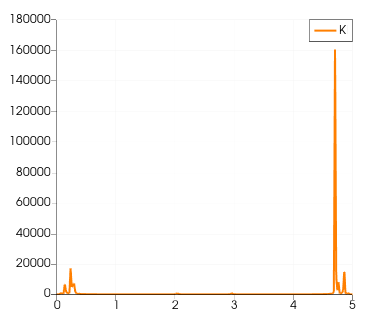
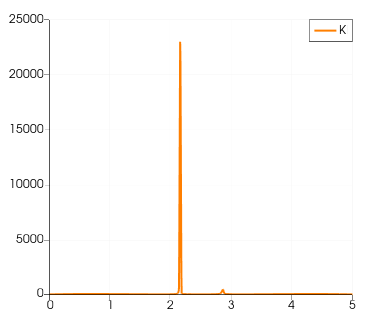
It indicates that,

For steady flow, the two eddies at the rear of the cylinder do not contribute to flow instability or the formation of the Karman vortex street.
The formation of the Karman vortex street is primarily due to the interaction of two shear layers on either side of the cylinder and the absolute instability in the cylinder's wake.
The instability primarily occurs in the wake and near the wall of the cylinder, rather than in the incoming flow. The peak K values are most prominent in the middle of the wake, suggesting potential areas of instability.

Reference

[1] Taneda, S., Experimental investigation of the wakes behind cylinders and plates at low Reynolds numbers, Journal of Physical Society of Japan, vol.11, pp.302-307, 1956.

[2] Taneda, S., Downstream development of the wakes behind cylinder, Journal of Physical Society of Japan, vol.14, pp.843-848, 1959.

[3] Zdravkovich, M. M., Flow around circular cylinders, Vol. 1: Fundamentals. Oxford: Oxford University Press, 1997.

[4] Dou, H.-S., Mechanism of flow instability and transition to turbulence, International Journal of Non-Linear Mechanics, vol.5, pp.512-517, 2006.

[5] Dou, H.-S., Khoo, B.C., and Yeo K.S., Instability of Taylor-Couette flow between concentric rotating cylinders, International Journal of Thermal Science, vol.47, pp.1422-1435, 2008.

[6] Noack, Bernd R., and Helmut Eckelmann, A Global Stability Analysis of the Steady and Periodic Cylinder Wake, Journal of Fluid Mechanics, vol. 270, pp. 297–330, 1994.